【導(dǎo)讀】有了上一節(jié)的基礎(chǔ)，這一節(jié)我們來(lái)看看D類(lèi)音頻功放的LC濾波器如何設(shè)計(jì)，思路是怎么樣的，可以看作是一個(gè)案例?？紤]到有些同學(xué)沒(méi)接觸過(guò)D類(lèi)音頻功放，我會(huì)先簡(jiǎn)單介紹下D類(lèi)功放的工作原理，然后D類(lèi)功放為什么要用LC濾波器，再到LC濾波器設(shè)計(jì)具體過(guò)程。
LC串聯(lián)諧振的意義
有了上一節(jié)的基礎(chǔ)，這一節(jié)我們來(lái)看看D類(lèi)音頻功放的LC濾波器如何設(shè)計(jì)，思路是怎么樣的，可以看作是一個(gè)案例。
考慮到有些同學(xué)沒(méi)接觸過(guò)D類(lèi)音頻功放，我會(huì)先簡(jiǎn)單介紹下D類(lèi)功放的工作原理，然后D類(lèi)功放為什么要用LC濾波器，再到LC濾波器設(shè)計(jì)具體過(guò)程。
TI公司也有介紹D類(lèi)放大器LC濾波器的設(shè)計(jì)文檔，文末會(huì)分享出來(lái)。我寫(xiě)的與TI的區(qū)別，TI的主要介紹具體如何設(shè)計(jì)，我主要想說(shuō)明思路過(guò)程，并指出里面的一些細(xì)節(jié)，為什么是這樣。我希望的是，有了思路，即使沒(méi)有任何文檔，遇到類(lèi)似的問(wèn)題，也能自己去分析。
D類(lèi)功放工作原理
D類(lèi)功放相對(duì)于A，B，C類(lèi)來(lái)說(shuō)更不好理解，因?yàn)樗切枰{(diào)制的，看起來(lái)就是占空比不同的PWM波，波形看著與我們的音頻模擬波形一點(diǎn)都不像。
下面來(lái)看一看它的原理。
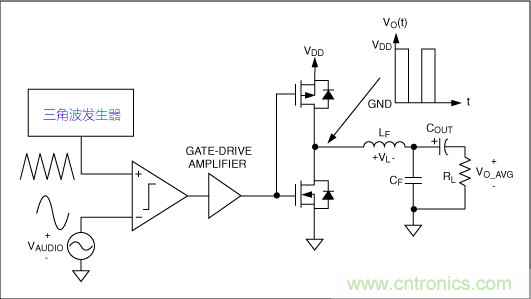
簡(jiǎn)單理解就是：音頻信號(hào)與三角波高頻載波經(jīng)過(guò)比較器進(jìn)行比較，得到占空比不同的PWM波，然后將得到PWM信號(hào)通過(guò)MOS管對(duì)管，經(jīng)過(guò)濾波器輸入到喇叭。調(diào)制后得到的PWM里面含有音頻分量，然后通過(guò)LC濾波器濾掉高頻載波還原成原始信號(hào)。
原理確實(shí)非常簡(jiǎn)單，但是我們可能會(huì)有如下問(wèn)題，僅僅理解以上內(nèi)容還是遠(yuǎn)遠(yuǎn)不夠的。
為什么有的電路喇叭兩端用示波器量就是PWM波，但是卻能正常發(fā)出聲音？
LC濾波器該如何設(shè)計(jì)，L，C如何取值？
有的D類(lèi)放大器要LC濾波，有的用磁珠就可以了，為什么？
還有的廠家的宣稱(chēng)它們的放大器不需要濾波，用了什么技術(shù)？
下面來(lái)看看這些問(wèn)題是怎么分析的。
典型的D類(lèi)放大器電路
D類(lèi)放大器，我們常用的方式是差分的方式，即兩個(gè)MOS對(duì)管中間接喇叭。下面就只分析這種差分方式，單端的分析方法也差不多。
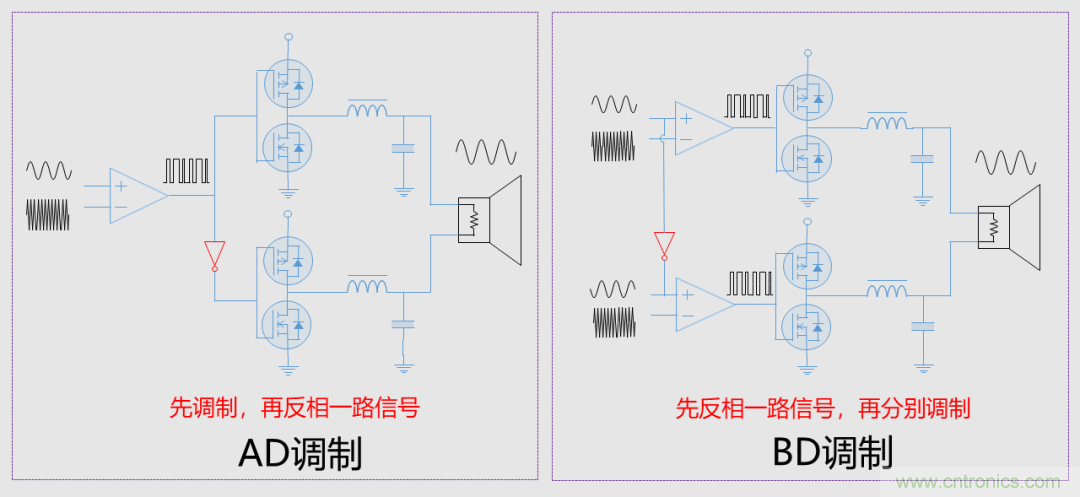
首先，D類(lèi)放大器是一個(gè)大類(lèi)，主要區(qū)別在于有不同的調(diào)制方式，下面先介紹兩種，AD類(lèi)，和BD類(lèi)。
AD類(lèi)是經(jīng)過(guò)三角波調(diào)制后再反相，用了一個(gè)比較器。BD類(lèi)是先將音頻信號(hào)反相，再將原信號(hào)和反相后的信號(hào)分別通過(guò)調(diào)制，用了兩個(gè)比較器，從圖中看不出來(lái)差別，下面來(lái)看看波形的區(qū)別。
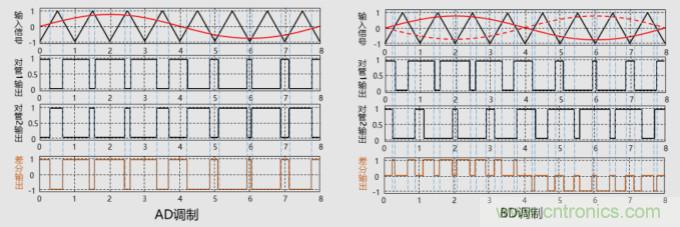
紅色的為音頻信號(hào)，三角波是調(diào)制信號(hào)，我們可以很容易的得到濾波之前的差分輸出信號(hào)。從波形上看到，AD與BD的差分輸出有著明顯的區(qū)別，但是二者的電平都是高低變化，我們沒(méi)法從上面直接得到有用的信息，比如看不出來(lái)哪種效率更高，哪種輻射會(huì)小一些等等。
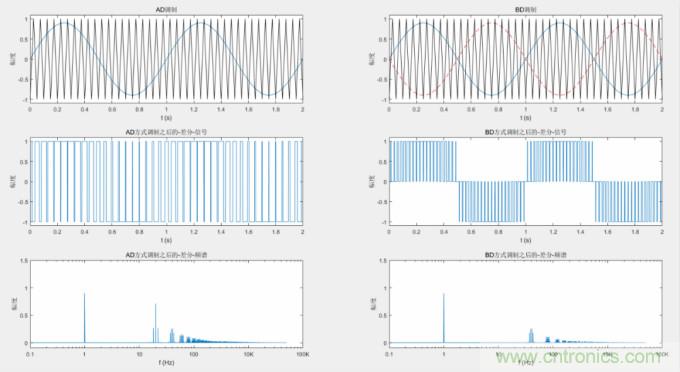
這時(shí)候，我之前的文章“信號(hào)在腦子里面應(yīng)該是什么樣的”就要派上用場(chǎng)了，我們需要把輸出信號(hào)進(jìn)行傅里葉變換，得到它們的頻譜，有了頻譜，就很容易看出差別。為此，我借助了Matlab軟件，分別畫(huà)出它們的頻譜。
注：為了減小Matlab軟件的計(jì)算量（計(jì)算量大了電腦會(huì)卡），我設(shè)定的音頻信號(hào)為1Hz，調(diào)制三角波為20Hz，雖然實(shí)際音頻信號(hào)頻率肯定是比1Hz要高的，但是分析結(jié)果應(yīng)是一樣的。
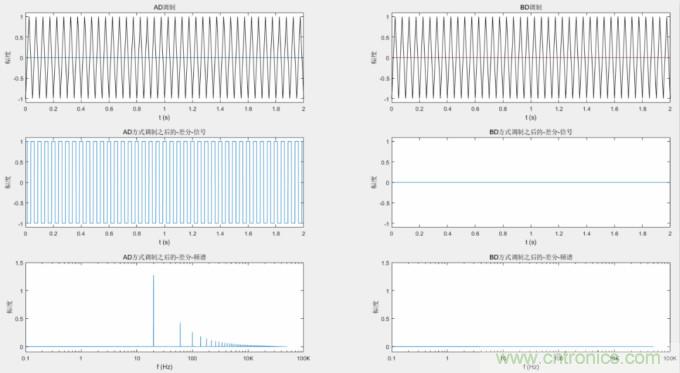
下圖是用幅度為1，頻率為20Hz的三角波，來(lái)調(diào)制幅度為0．9，頻率為 1Hz的正弦波。
從上圖看出，調(diào)制之后的有用信號(hào)1Hz被保留，幅度都是0．9，兩種方式都是一樣的，這說(shuō)明都能達(dá)到目的，包含了完整的音頻信號(hào)。
AD調(diào)制方式，除了有用信號(hào)1Hz在，還有調(diào)制三角波頻率20Hz的幅度也很大。而B(niǎo)D調(diào)制方式，20Hz頻率消失了，只存在更高的諧波。從這個(gè)角度說(shuō)， BD的方式是要更好的，損耗降低了。
在音頻輸入為0的時(shí)候，也就是說(shuō)放大器空閑，更能看出AD與BD的區(qū)別，如下圖：
在輸入為0的時(shí)候，AD方式的差分輸出為方波，而B(niǎo)D方式輸出為0，毫無(wú)疑問(wèn)，BD方式功耗更低。
事實(shí)上，我們拿到了頻譜，就能知道很多事情了。
首先，這些開(kāi)關(guān)信號(hào)實(shí)在看起來(lái)不像是模擬音頻信號(hào)，但是其確實(shí)包含了完整的音頻頻率信號(hào)在其中，所以直接通到喇叭也是可以正常響的，雖然額外多了高頻載波，但是頻率太高，超過(guò)人耳范圍，高頻分量是聽(tīng)不見(jiàn)的。
其次，這些開(kāi)關(guān)信號(hào)除了包含有用信號(hào)，還有豐富的高頻頻率，這些高頻頻率從調(diào)制頻率開(kāi)始往上。這些高頻分量通到喇叭是沒(méi)有什么好處的，反而會(huì)額外帶來(lái)功率損耗，還有會(huì)造成EMI的問(wèn)題。所以，我們需要一個(gè)濾波器來(lái)濾掉高頻分量。并且，因?yàn)轵?qū)動(dòng)喇叭需要的功率較大，而RC濾波器會(huì)有額外損耗，所以，LC低通濾波器就自然而然被選中了。
最后，我們知道頻譜里面的高頻的頻譜分布，那么濾波器的截止頻率自然就出來(lái)了。截止頻率必須高于音頻頻率上限20Khz，而要小于三角波的調(diào)制頻率，在這個(gè)范圍內(nèi)，截止頻率越低，去除高頻分量越好。
下面分享下上面波形的Matlab源碼，有興趣的同學(xué)可以去試試。
f＿audio＝1； ％被調(diào)制信號(hào)（音頻信號(hào)）頻率為1Hz
f＿sanjiao＝20； ％三角波調(diào)制頻率為20Hz
％％％％％％％％％％％％％％％％％％％％％％％％ fft采樣設(shè)置
Fs＝10000； ％采樣率為Fs
L＝（Fs／f＿audio）＊100；
％信號(hào)長(zhǎng)度（采樣總點(diǎn)數(shù)）：100個(gè)周期的信號(hào)，長(zhǎng)度越長(zhǎng)，fft精度越高，但是執(zhí)行時(shí)間越長(zhǎng)
T＝1／Fs； ％采樣周期
t＝（0：L）＊T； ％時(shí)間長(zhǎng)度
A＿audio ＝ 0．9； ％音頻信號(hào)的幅度為 0．9－－－－可以修改為不同的值嘗試
S1＝A＿audio＊sin（2＊pi＊f＿audio＊t）； ％被調(diào)制信號(hào)（音頻信號(hào)）為幅度A＿audio的正弦波
S2＝sawtooth（2＊pi＊f＿sanjiao＊t，0．5）； ％調(diào)制信號(hào)（三角波）為幅度為1的三角波
N＝length（t）；
PWM1＝zeros（1，N）； ％定義PWM1的長(zhǎng)度 AD調(diào)制后差分波形
PWM2＝zeros（1，N）； ％定義PWM2的長(zhǎng)度 BD調(diào)制后差分波形
tmp＝zeros（1，N）； ％定義tmp的長(zhǎng)度 計(jì)算用（中間變量）
for i＝1：N
if S1（i）＞S2（i）
PWM1（i） ＝ 1；
tmp（i） ＝ 1；
else
PWM1（i） ＝ －1；
tmp（i） ＝ 0；
end
end
for i＝1：N
if －S1（i）＞S2（i）
PWM2（i） ＝ tmp（i）－1；
else
PWM2（i） ＝ tmp（i）；
end
end
％％％％％％％％％％％％％％％％％％％％％％％％ AD調(diào)制
subplot（3，2，1）；
plot（t，S1，t，S2，＇k＇）；
set（gca，＇XLim＇，［0 2／f＿audio］）；％x軸的數(shù)據(jù)顯示基頻2個(gè)周期
set（gca，＇YLim＇，［－1．1 1．1］）；
title（＇AD調(diào)制＇）；
xlabel（＇t （s）＇）；
ylabel（＇幅度＇）；
subplot（3，2，3）；
plot（t，PWM1）；
set（gca，＇XLim＇，［0 2／f＿audio］）；％x軸的數(shù)據(jù)顯示范圍
set（gca，＇YLim＇，［－1．1 1．1］）；
title（＇AD方式調(diào)制之后的－差分－信號(hào)＇）；
xlabel（＇t （s）＇）；
ylabel（＇幅度＇）；
X1＝abs（fft（PWM1））；
subplot（3，2，5）；
semilogx（Fs＊（0：（L／2））／L，X1（1：L／2＋1）＊2／L）；
set（gca，＇XLim＇，［0．1 10000］）；％x軸的數(shù)據(jù)顯示范圍
set（gca， ＇XTickLabel＇ ，｛＇0．1＇，＇1＇，＇10＇，＇100＇，＇10K＇，＇100K＇｝）； ％x軸頻率數(shù)據(jù)
title（＇AD方式調(diào)制之后的－差分－頻譜＇）；
set（gca，＇YLim＇，［－0．1 1．5］）；
xlabel（＇f （Hz）＇）；
ylabel（＇幅度＇）；
％％％％％％％％％％％％％％％％％ BD調(diào)制差分信號(hào)
subplot（3，2，2）；
plot（t，S1，t，－S1，＇－－r＇，t，S2，＇k＇）；
set（gca，＇XLim＇，［0 2／f＿audio］）；％x軸的數(shù)據(jù)顯示基頻2個(gè)周期
set（gca，＇YLim＇，［－1．1 1．1］）；
title（＇BD調(diào)制＇）；
xlabel（＇t （s）＇）；
ylabel（＇幅度＇）；
subplot（3，2，4）；
plot（t，PWM2）；
set（gca，＇XLim＇，［0 2／f＿audio］）；
％x軸的數(shù)據(jù)顯示范圍set（gca，＇YLim＇，［－1．1 1．1］）；
title（＇BD方式調(diào)制之后的－差分－信號(hào)＇）；
xlabel（＇t （s）＇）；
ylabel（＇幅度＇）；
X2＝abs（fft（PWM2））；
subplot（3，2，6）；
semilogx（Fs＊（0：（L／2））／L，X2（1：L／2＋1）＊2／L）；
set（gca，＇XLim＇，［0．1 10000］）； ％x軸的數(shù)據(jù)顯示范圍
title（＇BD方式調(diào)制之后的－差分－頻譜＇）；
set（gca， ＇XTickLabel＇ ，｛＇0．1＇，＇1＇，＇10＇，＇100＇，＇10K＇，＇100K＇｝）； ％x軸頻率數(shù)據(jù)
set（gca，＇YLim＇，［－0．1 1．5］）；
xlabel（＇f （Hz）＇）；
ylabel（＇幅度＇）；
小結(jié)
這一節(jié)我們看了Class D的輸出信號(hào)波形，并分析了其頻譜，我們要學(xué)會(huì)看頻譜。本節(jié)就先寫(xiě)到這里吧，下一節(jié)會(huì)具體看看LC濾波器的設(shè)計(jì)過(guò)程。
來(lái)源：硬件工程師煉成之路
免責(zé)聲明：本文為轉(zhuǎn)載文章，轉(zhuǎn)載此文目的在于傳遞更多信息，版權(quán)歸原作者所有。本文所用視頻、圖片、文字如涉及作品版權(quán)問(wèn)題，請(qǐng)聯(lián)系小編進(jìn)行處理。
推薦閱讀：
